基本概念

一元积分（单变量积分）$ \int f(x) \, dx $，几何意义通常是计算曲线 $y = f(x)$ 下方 x轴上某个区间 [a, b] 内的面积，可以视为在一维区间上的 面积累加

二重积分的几何意义是计算函数 $f(x, y)$ 在某个二维区域 D 上方的体积（或者面积的累加）。这可以视为在二维区域上的体积累加或面积累加，特别是当 $f(x, y)$ 是一个高度函数时，它代表区域 D 上方某个立体的体积。

分部积分法

分布积分

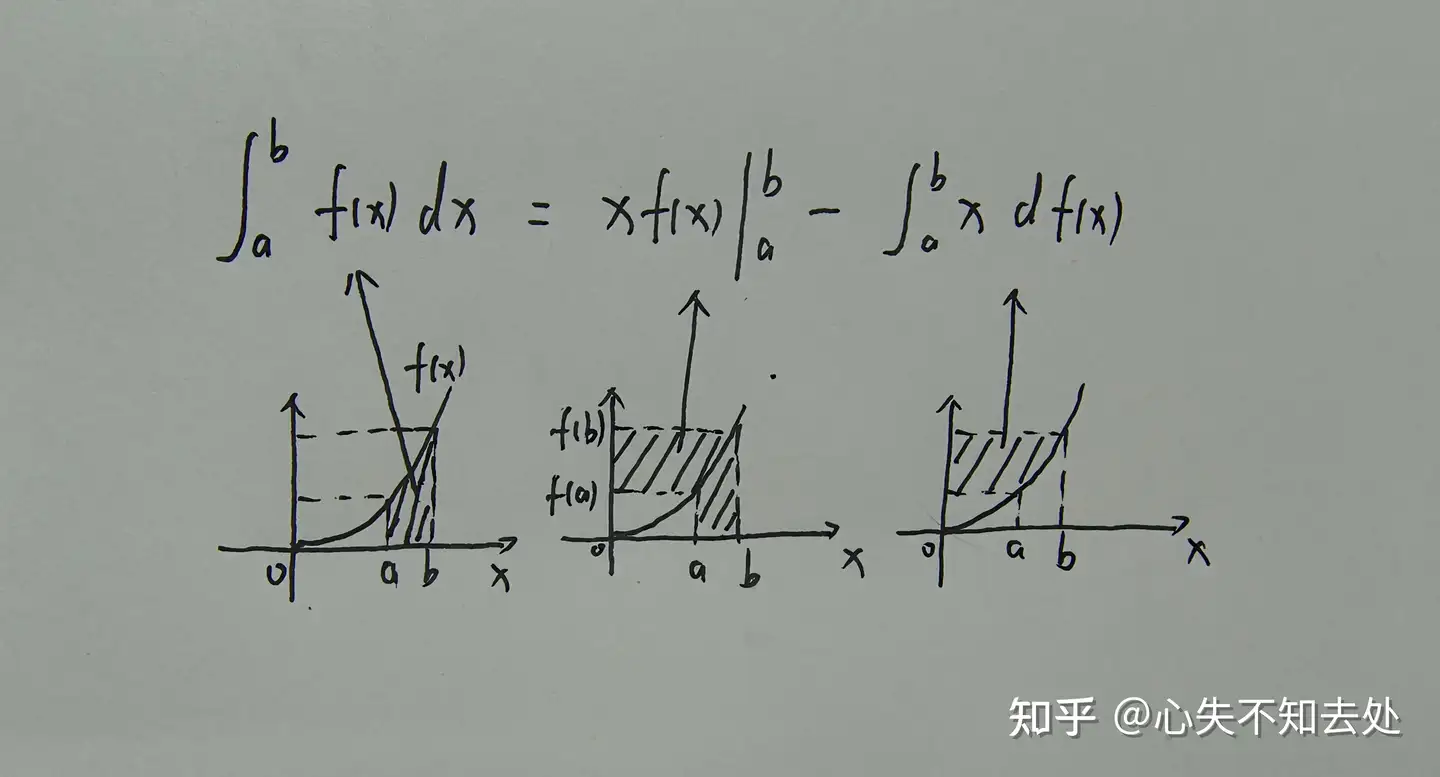
例题：$ \int x e^x \, dx $

看到函数乘积时，可以尝试分部积分法。这里 $x $ 是多项式，容易微分； $e^x $ 是指数函数，容易积分，因此选择分部积分法。

设 $u = x ， dv = e^x \, dx $，$ du = dx, \quad v = e^x$，根据分部积分公式： $ \int u \, dv = uv - \int v \, du $

$$ \int x e^x \, dx = x e^x - \int e^x \, dx = x e^x - e^x + C = e^x(x - 1) + C $$

例题：$ \int \sqrt{1 - x^2} \, dx $

遇到根号下有 $ 1 - x^2 $ 这样的表达式，令 $ x = \sin \theta $，则 $ dx = \cos \theta \, d\theta $

$$ \int \sqrt{1 - \sin^2 \theta} \cos \theta \, d\theta = \int \cos^2 \theta \, d\theta $$

再利用 $ \cos^2 \theta = \frac{1 + \cos 2\theta}{2} $

$$ \int \frac{1 + \cos 2\theta}{2} \, d\theta = \frac{\theta}{2} + \frac{\sin 2\theta}{4} + C $$

回代 $ \theta = \arcsin x $，得到结果。

例题：$ \int \frac{2x + 3}{x^2 - x - 6} \, dx $

有理函数积分，多项式的比值，可以因式分解

$$ \frac{2x + 3}{(x - 3)(x + 2)} = \frac{A}{x - 3} + \frac{B}{x + 2} $$

通过解方程： A = 1 ， B = 1

$$ \int \frac{1}{x - 3} \, dx + \int \frac{1}{x + 2} \, dx = \ln |x - 3| + \ln |x + 2| + C $$

例题：$ \int \frac{2x}{x^2 + 1} \, dx $

被积函数的分子是分母的导数形式，设 $u = x^2 + 1 $ ，则 $du = 2x \, dx $

$$ \int \frac{2x}{x^2 + 1} \, dx = \int \frac{du}{u} = \ln |u| + C = \ln (x^2 + 1) + C $$

毫无技术可言，缓存就是了，空间换时间

$$ \int \frac{1}{\sqrt{1 - x^2}} \, dx \Rightarrow \int \frac{1}{\sqrt{1 - x^2}} \, dx = \arcsin(x) + C $$