基础概念
它扩展了单变量函数的微积分概念到多变量的环境,可以描述现实世界中许多复杂的场景,假设我们有一个薄的平面板,其密度不均匀,密度函数为 $\rho(x, y)$ ,表示在平面上任意点 $ (x, y) $处的密度(单位为质量/单位面积)。我们希望计算这个平面板的总质量。
定义问题:设平面板的形状为矩形区域 D ,其边界是 $a \leq x \leq b$ 和 $c \leq y \leq d$ 。密度函数 $\rho(x, y)$ 给出在 $(x, y)$ 处的密度。
具体来说,若 D 是矩形区域 $[a, b] \times [c, d]$ ,二重积分表示为:
$$ M = \int_c^d \int_a^b \rho(x, y) \, dx \, dy $$
实际计算,假设密度函数是 $\rho(x, y) = 2x + 3y$ ,而区域 D 是矩形区域 $[0, 2] \times [0, 3]$,那么,总质量 M 计算如下:
$$M = \int_0^3 \int_0^2 (2x + 3y) \, dx \, dy$$
偏导数
偏导数是指多元函数对某一个变量的导数,其他变量保持不变。假设有一个函数 $ f(x, y)$ ,其相对于 $x$ 的偏导数表示为 $\frac{\partial f}{\partial x}$ ,相对于 $y$ 的偏导数表示为 $\frac{\partial f}{\partial y}$ 。
例如,对于函数 $f(x, y) = x^2 + y^2$ ,其对 $x$ 的偏导数为:
$$\frac{\partial f}{\partial x} = 2x$$
而对 $y$ 的偏导数为:
$$\frac{\partial f}{\partial y} = 2y$$
偏微分
多元函数在某一变量发生微小变化时,函数值的微小变化量。它实际上是偏导数乘以微小增量
如果 $z = f(x, y)$ ,那么 $x$ 方向的偏微分表示为 $\frac{\partial f}{\partial x} dx$ ,而 $y$ 方向的偏微分表示为 $\frac{\partial f}{\partial y} dy $
全微分
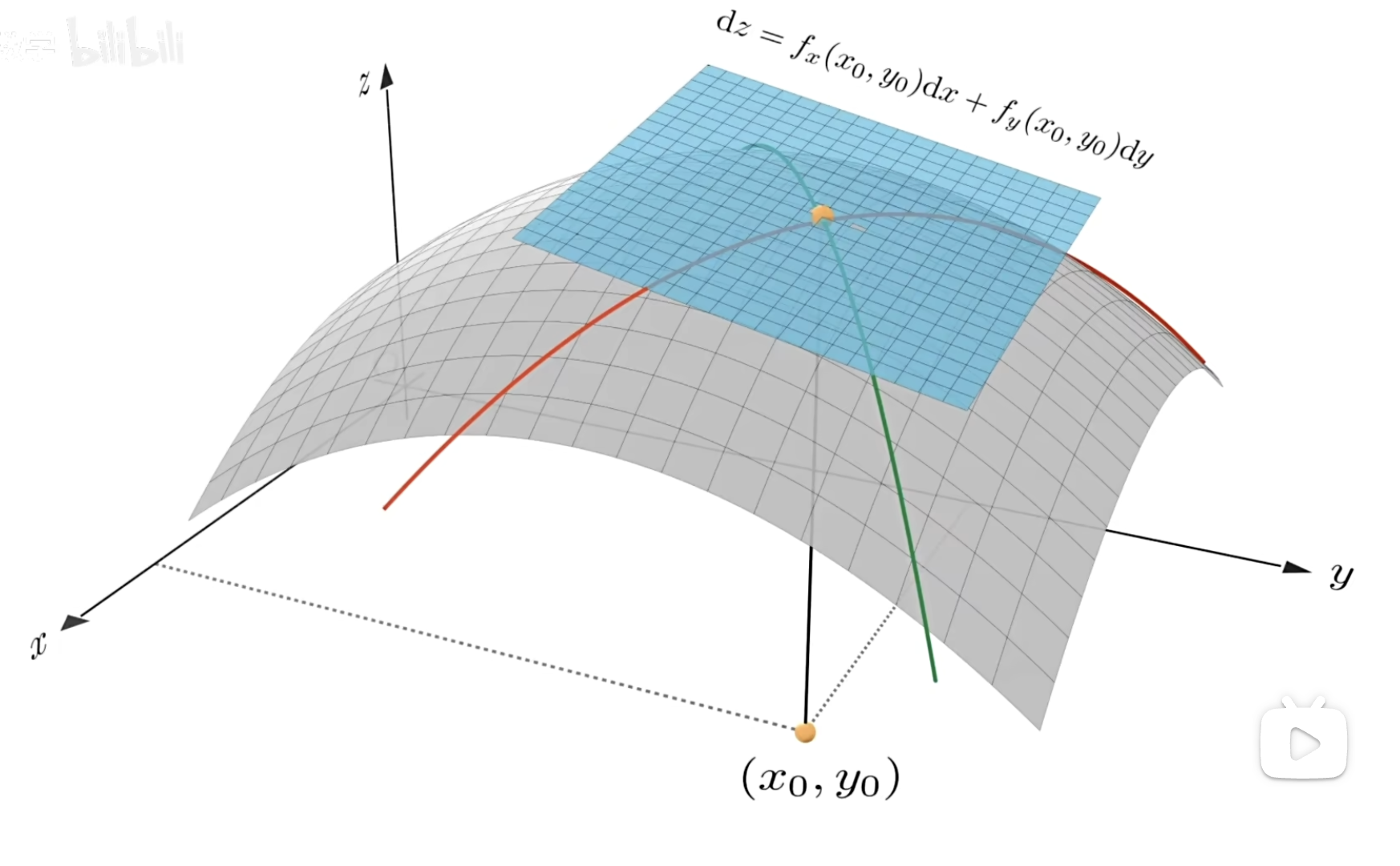
多个变量的微分求和,假设有一个多变量函数 $z = f(x, y)$ ,其中 $x$ 和 $y$ 是自变量,那么 $f(x, y)$ 的全微分 $dz$ 表达式为
$$ dz = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy $$
其中,$\frac{\partial f}{\partial x}$ 是函数 $f$ 对 $x$ 的偏导数。$\frac{\partial f}{\partial y} $是函数 $f$ 对 $y$ 的偏导数。$dx$ 和 $dy$ 是自变量 $x$ 和 $y$ 的微小增量。
例题: $z = f(x, y) = x^2 + 3xy + y^2$ 。
对 $x$ 求偏导数:
$$ \frac{\partial f}{\partial x} = 2x + 3y$$
对 $y$ 求偏导数:
$$ \frac{\partial f}{\partial y} = 3x + 2y$$
写出全微分:
$$ dz = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy $$
将偏导数代入,得到:
$$ dz = (2x + 3y) dx + (3x + 2y) dy $$
常微分方程(普通微分方程)
常微分方程(Ordinary Differential Equation, ODE)之所以叫“常微分方程”,是为了将其与“偏微分方程”(Partial Differential Equation, PDE)区分开来。这个名称反映了它们涉及的微分运算的不同性质和复杂性。偏微分方程中的“偏”表示方程中的微分操作涉及多个自变量。
常微分方程中的“常”表示的是方程中的微分操作只涉及一个自变量。因此,方程中的微分称为“常微分”,例如,经典的一阶常微分方程可以写成: $\frac{dy}{dx} = f(x, y)$
阶数
一阶:$ \frac{dy}{dx} = 3x + 2y $
二阶:$ \frac{d^2y}{dx^2} - 4y = 0 $
高阶: $ \frac{d^3y}{dx^3} + y = \sin(x) $
线性与非线性
在一个微分方程中,如果未知函数 $y$ 和它的导数 $y{\prime}$ 以线性形式出现,即它们都是一次幂且没有乘积或其他非线性形式(如 $y^2$ 或 $y \cdot y{\prime}$ ),那么这个方程就是线性的。
线性:$ \frac{dy}{dx} + 2y = e^x $
非线性:$ \frac{dy}{dx} = y^2 + x $
方程形式
在英文中,“homogeneous” 这个词来源于希腊语“homos”,意思是“相同的”。对于齐次方程,所有项要么都是零,要么是有关联的(线性组合),因此它们被看作是“相同的”类型。
齐次:所有项都是未知函数的导数或未知函数的线性组合(即没有独立的非零常数项)
齐次:$ y{\prime}{\prime} + 2y{\prime} + y = 0 $
非齐次:$ y{\prime}{\prime} + 2y{\prime} + y = e^x $
解的显式性
将方程解为 $y$ 或其导数的显式形式
显示解:$ \frac{dy}{dx} = 2x + 3 $
隐式:$ y \frac{dy}{dx} = x^2 + y^2 $
系数性质(常、变)
二阶常系数:$ y{\prime}{\prime} - 3y{\prime} + 2y = 0 $
二阶变系数:$ x^2 y{\prime}{\prime} + x y{\prime} - y = 0 $
可解性
判断一个常微分方程是否可解,尤其是能否通过解析方法得到显式解,通常需要依靠经验、已有的解法理论以及对方程形式的分析。以下是一些常用的判断方法和原则:
分离变量法:适用于可以将方程的变量分离的情况。
示例: $\frac{dy}{dx} = xy $
解法:将方程改写为 $\frac{1}{y} dy = x dx $ ,然后两边分别积分,得到 $\ln |y| = \frac{x^2}{2} + C $ ,从而可以得到显式解 $y = Ce^{x^2/2}$ 。
积分因子法:适用于线性一阶微分方程。
示例: $ \frac{dy}{dx} + P(x)y = Q(x) $
解法:通过引入一个积分因子 $\mu(x) = e^{\int P(x)dx}$ ,可以使方程变为可积分形式。
特征方程法:用于常系数线性微分方程。
示例: $y{\prime}{\prime} - 3y{\prime} + 2y = 0 $
解法:求特征方程的根,得到通解。